Darío Maravall Casesnoves

VERITAT I REALITAT DE LES GEOMETRIES EUCLIDIANES I NO EUCLIDIANES

És per a mi un gran honor el que m'ha concedit la Universitat Politècnica de València en nomenar-me doctor honoris causa, tant pel gran prestigi d'aquesta Universitat com per com de preuat és el títol.

A més a més, en el meu cas és també una gran satisfacció per com d'unit estic a aquesta terra valenciana; sóc de Xàtiva, ho van ser els meus pares, els meus avis i tots els meus avantpassats que jo recorde.
He emprat en plural la paraula geometries euclidianes perquè a banda de l'espai habitual, la geometria euclidiana pot adequar-se a espais que no són simplement connexos, que encara que tenen la mateixa mètrica, tenen propietats topològiques distintes; de manera que existeixen figures geomètriques d'aparença surrealista, amb estranyes propietats. També les geometries hiperbòlica i el·líptica (no euclidianes) poden adequar-se a espais que no són simplement connexos, cosa que té aplicacions físiques. Vegeu els dibuixos i la bibliografia.

Analitzaré alguns aspectes de les matemàtiques i de la física, i també de les seues filosofies, alguns dels quals em semblen rellevants, i d'altres, curiosos.

Assenyalaré el seu impacte en les nostres formes de pensament i en la nostra concepció ideològica del món. Una característica que cal assenyalar és com ha anat canviant en el temps la nostra idea de la veritat, de la realitat de les coses, de què és una demostració, etc. La veritat ha perdut en el camp científic una part del seu valor absolut, s'ha relativitzat un poc, en el sentit que ho va entendre el gran literat italià Pirandello, i que ha constituït el nucli d'algunes de les seues més cèlebres obres de teatre: Sis personatges a la recerca d'autor , Enric IV i,sobretot, Així és si així us sembla . Aquesta última obra ha sigut traduïda a l'espanyol per Ildefonso Grande, que va ser catedràtic de francés a l'Institut de Xàtiva, amb el títol La verdad de cada cual , títol molt apropiat, i que traslladat al camp de la ciència ens faria dir que cada època té la seua veritat científica, el seus propis mètodes per a arribar a aquesta veritat i el seus criteris per a mesurar l'exactitud i el rigor en les demostracions.

Nosaltres, els occidentals, som hereus directes de la cultura grega i romana, herència que ha sigut modificada i molt millorada per la que hem rebut del cristianisme. Els grecs ens van deixar tres grans llegats científics que han durat segles, que són la física i la lògica d'Aristòtil i la geometria d'Euclides, la primera falsa i les altres dues vertaderes. La física d'Aristòtil va associada, encara que no per necessitat lògica, a la teoria geocèntrica de Ptolemeu; les dues són falses, però, a pesar d'això, la segona va produir un gran progrés en l'astronomia mentre es va creure en ella. És sorprenent com el gran talent i enginy dels antics va fer possible que a pesar de recolzar-se en una base falsa obtingueren un coneixement tan gran dels fets reals. La fi de la física aristotèlica i del sistema de Ptolemeu té lloc amb Galileu. El procés històric que conduí a aquest final és apassionant. L'hem descrit i analitzat en una conferència publicada el 1993 per Los Amigos de la Cultura Científica que porta per títol "El legado de Galileu en la evolución de la física hasta hoy", per la qual cosa no insistiré en aquest tema.

La lògica aristotèlica continua sent vàlida, ha regnat pràcticament sense rival fins a final del segle XIX, en què naix la lògica matemàtica, i a partir d'ací ha tingut lloc el floriment de les lògiques no aristotèliques. En la lògica d'Aristòtil són vàlids dos grans principis que tenen un ús freqüent i molt important en la matemàtica, que són el principi de contradicció segons el qual "una proposició no pot ser vertadera i falsa alhora" i el principi del tercer exclòs, segons el qual "una proposició és o vertadera o falsa", també anomenat principi del tertium non datur . Modernament Brower desenvolupà l'anomenada lògica intuïcionista, que nega el principi del tercer exclòs, i jo mateix he desenvolupat una lògica que he proposat anomenar lògica relativista, en la qual no és vàlid el principi de contradicció (vegeu la bibliografia). Amb relació a allò que he anomenat lògica relativista, he de fer una citació que no coneixia quan vaig publicar els meus escrits. Aquesta citació és de Coleridge en les seues Xarrades de sobretaula, que escriu: "Plató ens fa veure que proposicions relatives a concepcions contradictòries són, tanmateix, vertaderes, i per tant han de pertànyer a una lògica superior, la de les idees. Són contradictòries només en la lògica aristotèlica, que és l'instint de la comprensió" (citació resumida).

El sil·logisme és una peça clau de la lògica aristotèlica. En analitzar la paradoxa de Zenó d'Elea d'Aquil·les i la tortuga, en allò que he anomenat els enganys de la raó (vegeu la bibliografia), he assenyalat que en lògica, com en matemàtiques, hi ha el perill en l'ús de l'infinit i he establit que un sil·logisme repetit infinites vegades pot deixar de ser un sil·logisme, o el que és el mateix: que una demostració repetida infinites vegades pot deixar de ser una demostració.

Els grecs van progressar molt més en matemàtiques que en física, i dins de les matemàtiques el progrés va ser major en geometria. Al segle VI aC a Milet, que era un port i una ciutat jònica, va florir per primera vegada el pensament filosòfic i científic grec. Milet va ser conquerida pels perses l'any 540 aC i va tenir una relativa autonomia fins al 494, en què va revoltar-se contra Pèrsia i va ser vençuda. Va ser alliberada el 479, però en aquesta època ja havia perdut la seua importància cultural a favor de la Grècia europea, especialment d'Atenes. A Milet va viure Tales (625-547?), el primer en el temps dels grans filòsofs grecs, a qui s'atribueix el càlcul de les altures de les piràmides egípcies mitjançant les propietats dels triangles semblants, el descobriment del poder d'atracció dels imants i de l'electricitat estàtica. Ell va iniciar la transformació de les matemàtiques en una ciència abstracta i va fer les primeres demostracions deductives d'alguns teoremes.

Abans d'arribar a Euclides, entre molts altres savis van destacar Pitàgores (570-480?), que en l'ordre cronològic va ser el primer físic matemàtic en donar a conéixer la relació entre la longitud de les cordes i les notes musicals; és considerat el fundador de la matemàtica pura, en reconéixer que els nombres i les figures geomètriques són idees produïdes per la ment humana, distintes de les imatges físiques, de caràcter abstracte totalment deslligat de la matèria. L'aportació més important de Pitàgores és el teorema que duu el seu nom, el qual afirma que el quadrat de la hipotenusa és igual a la suma dels quadrats dels catets. A banda del seu gran interés teòric, és una teorema amb moltes aplicacions pràctiques al càlcul de la diagonal del quadrat en funció del costat, de la diagonal del cub en funció de l'aresta, del costat del triangle equilàter en funció del radi del cercle circumscrit. Unit a aquest descobriment hi ha el fet que no existeix cap nombre racional el quadrat del qual siga igual al doble d'un quadrat, o el que és el mateix, que œ no és un nombre racional (és irracional), és a dir, no és igual al quocient de dos nombres enters. Combinat amb el descobriment posterior de la descomposició d'un quadrat en la suma de dos quadrats i dos rectangles iguals, que és la demostració geomètrica del quadrat d'una suma, serveix per a calcular el costat d'un triangle qualsevol en funció dels altres dos i de la projecció d'un d'ells sobre l'altre.

La importància actual del teorema de Pitàgores és molt gran perquè, aplicat a quantitats infinitesimals, defineix la mètrica de les superfícies en l'espai euclidià, i dels espais riemannians (no euclidians); és la base de la geometria diferencial mètrica.

Convé assenyalar que el teorema de Pitàgores no és vàlid en les geometries no euclidianes clàssiques; en la hiperbòlica el quadrat de la hipotenusa és més petita que la suma dels quadrats dels catets, i en l'el·líptica és major. El primer resultat és important en física, en la cinemàtica relativista, en què la composició de velocitats coplanàries no és commutativa, i existeix una velocitat superior límit (la velocitat de la llum en el buit). (Vegeu la bibliografia).

Un altre matemàtic important anterior a Euclides fa ser Èudox de Cnidos (408-355), el qual va establir segurament per primera vegada, d'una manera clara, l'estructuració deductiva de la geometria sobre la base d'axiomes explícits; per a ell, com per a Plató ( teoria de l'anamnesi ), la ment era capaç de reconéixer com a veritats evidents els axiomes. Les seues aportacions científiques van ser molt variades i importants tant en geometria com en astronomia i geografia. Va preparar d'una manera molt eficaç el camí a Euclides. Èudox va ser un platònic; Euclides va ser alhora un platònic i un aristotèlic.

Plató (427-347) i Aristòtil (384-322), encara que cap dels dos no van ser matemàtics, van contribuir molt al desenvolupament de la matemàtica grega, com a animadors i com a orientadors.
Plató va fundar a Atenes cap al 387 aC l'Acadèmia, que va ser una espècie d'universitat. És molt coneguda en l'Acadèmia la cèlebre frase "Que no hi entre qui no sàpiga geometria". Era un entusiasta de la matemàtica i creia que era molt important l'estudi d'aquesta per a l'aprenentatge de la filosofia i per al coneixement del món que ens envolta. Per a ell, els objectes geomètrics són independents de l'experiència i distints dels objectes físics; la seua realitat és intrínseca a ells. Plató va contribuir molt a la preferència dels grecs pels aspectes abstractes i per la veritat absoluta, encarnada per a ells en els teoremes matemàtics, la qual cosa els va fer molt exigents per al rigor i l'exactitud matemàtica.

L'Acadèmia de Plató va durar molt de temps. Als segles III i IV hi ha un renaixement del neoplatonisme, que es converteix, en part, en una reacció tardana del món romà pagà contra el cristianisme, que es fa molt fort sota l'emperador Julià l'Apòstata (331-363) també neoplatònic, però dura poc. L'any 529 l'emperador bizantí Justinià tanca l'Acadèmia d'Atenes, quan ja pràcticament el neopaganisme havia mort; és més aviat un acte simbòlic que recorda un poc el tancament del Club dels Jacobins de París el 1799 per Fouché, ministre del Directori (3 de Termidor), acte que al seu temps va semblar a l'opinió pública atrevit i quasi temerari com a consolidació de la reacció termidoriana, però que en realitat va ser també un acte simbòlic, ja que el Terror a París havia arribat a la seua fi el 9 de Termidor de 1794 amb la caiguda i mort de Robespierre i de la seua facció.

Com a record del sentiment d'adhesió de Plató a la geometria, fa uns quants anys a Madrid, un grup d'enginyers i científics van crear allò que anomenaven l'Akadèmia (amb k) Neoplatònica amb el lema "entre qui estime la geometria", per tal de renovar l'estudi i l'estima per aquesta ciència.

Aristòtil, en crear la lògica com una ciència deductiva (el seu Organon ) va contribuir enormement al pla del elements d'Euclides. Discrepava de Plató sobre la naturalesa dels objectes matemàtics, atribuïa la realitat de l'univers a la matèria, a les substàncies concretes, però entre les propietats dels objectes materials hi havia els nombres i les figures geomètriques, de manera que aquests són conceptes abstractes que es deriven de les propietats físiques dels cossos concrets.

Aristòtil va donar un concepte de definició que és pràcticament el modern, ha d'expressar-se en termes d'una cosa prèvia a allò que es defineix, reconeix la necessitat que hi haja uns pocs termes indefinits com a punt de partida per al conjunt de definicions. Aristòtil va adonar-se que una definició diu el que és una cosa, però no prova l'existència de la cosa. L'existència ha de demostrar-se excepte per a unes poques coses que serveixen de punt de partida per a l'elaboració de qualsevol teoria.

Aristòtil destaca la diferència entre els axiomes, que són veritats comunes a totes les ciències, i els postulats, que són veritats específiques d'una ciència particular. Pla que Euclides segueix en els seus Elements .

Abans que Euclides escriguera els seus Elements , uns altres grecs havien escrit els seus elements de geometria; entre aquests hi ha Hipòcrates, que va viure cap al 450 aC, i segurament va ser el primer grec que va escriure un tractat de geometria ( Lúnules hipocràtiques ); i Theudius de Magnèsia, el llibre del qual era text a l'Acadèmia de Plató. La idea que anava obrint-se camí era obtenir mitjançant la demostració (per via deductiva) el major nombre de veritats geomètriques i al mateix temps reduir al mínim les veritat primàries, reconegudes sense demostració, que servien com a punt de partida per al coneixement geomètric.

Euclides va viure de final del segle IV a principi del segle III aC; va ensenyar a Alexandria, centre intel·lectual de primera categoria en aquell temps, va ser deixeble de Plató i sens dubte va ser molt influït per Aristòtil. Cap al 300 aC va escriure els seus Elements ( Stoiecheia ) on va recopilar quasi tot el saber geomètric del seu temps, amb grans aportacions pròpies. És una obra supermestra.

El text grec ens ha arribat a través de molts manuscrits, la major part còpia d'una versió feta per Teó d'Alexandria al segle IV. El 1808 Peyrard va trobar al Vaticà un manuscrit del segle X que contenia una còpia anterior a la versió de Teó. També es van descobrir en altres biblioteques més manuscrits amb còpies de fragments d'altres versions, la qual cosa, juntament amb les traduccions àrabs i llatines, ha permés reconstruir quasi íntegrament el text original d'Euclides. Una de les versions més dignes de crèdit és la de Heiberg i Menge en vuit volums (Leipzig, 1883-1916) que conté les obres conegudes d'Euclides. Una altra és la de Heiberg (Cambridge, 1925) en tres volums, reimpresa el 1956 a Nova York).

Euclides des d'un principi va exercir una gran influència amb els seus Elements , i va ser molt comentat pels mateixos grecs, entre els quals Posidoni i Gèmino al segle I aC, Heró d'Alexandria dels segles I aC i I de la nostra era, Porfiri (segle III), Pappos d'Alexandria (final del segle III), Procle (410-485), Simplici, el comentador d'Aristòtil (segle VI), etc.
Molt prompte els àrabs van tenir coneixements dels Elements i van fer-ne traduccions a partir del segle VIII, sota el califat abbàssida de Bagdad, de Harun al Rashid (786-809).

Euclides va arribar a l'occident europeu principalment a partir de les seues traduccions al llatí a Toledo i Palerm, ciutats que van ser reconquerides als àrabs el 1085 i 1091, on a més d'Euclides es va traduir Aristòtil i Ptolemeu, i molt poc d'Arquimedes. D'aquesta manera, l'escola de traductors de Toledo va tenir un paper molt important en el desvetlament intel·lectual europeu del segle XII.

L'ús dels Elements d'Euclides com a text per a l'estudi de la geometria va durar moltíssim, fins ben entrat el segle XIX. Hi havia molt d'interés en el fet que s'estudiaren perquè pedagògicament no sols es volia que l'estudiant aprenguera geometria, sinó també perquè es considerava que el seu estudi era una bona gimnàstica mental i una manera de disciplinar el coneixement. Necessitats d'una altra classe van fer que a partir de final del segle XVII començaren a escriure's manuals de geometria per altres autors, els quals, encara que inspirats en Euclides, van introduir nous enfocaments i aportacions que van modificar bastant el text d'Euclides. Entre aquests manuals van ser importants a Anglaterra el de Simson de 1756, que va tenir vora trenta edicions, i el de Playfair de 1797, que en va tenir deu; a Alemanya, el de Lorenz de 1773; a França, el molt anterior de Déchales de 1672, que va ser diverses vegades reeditat i traduït a l'anglés i a l'italià; al segle XVIII, els Elements de Geometria de Legendre i de Lacroix a França.

No hi ha cap dubte que l'estudi de la geometria va apassionar molts estudiants (xiquets o adolescents) i que els va desvetlar una gran vocació. Va ser la forja de molts matemàtics cèlebres. Entre ells hi ha els casos de Pascal, en qui es mescla la història i la llegenda en la seua extraordinària precocitat matemàtica; Einstein, qui ell mateix conta que als 12 anys li va caure a les mans el que ell diu "el sant llibre de geometria" que li va causar una impressió indescriptible per la claredat i la precisió del text. És notable el cas de Galois, un dels més grans matemàtics. Va nàixer el 1811, el mateix any en què va nàixer el rei de Roma (el fill de Napoleó). El 1823, per tal de cursar estudis secundaris, va ingressar al col·legi reial Lluís el Gran, on Víctor Hugo i Robespierre havien estudiat. L'any següent Lluís XVIII moria i el seu germà Carles X, l'últim Borbó francés, era coronat. Amb l'adveniment d'aquest nou rei van tornar a França temps turbulents i revolucionaris que van influir en la vida de Galois. Aquest no es trobava a gust al col·legi, era conflictiu per als mestres, que el consideraven somnolent, indisciplinat i sense interés, però durant el curs de 1827 va haver d'estudiar els Elements de Geometria de Legendre i tot va canviar per a ell, va quedar concentrat i absort en la lectura d'aquest llibre, l'edifici de la geometria li va semblar una cosa plena de bellesa, els teoremes, més reals que el món físic; se li feia evident la veritat dels teoremes. Va aprendre en mesos un llibre destinat a ser estudiat en dos anys.

Tornant de nou a Euclides, hom el considera el pare de les matemàtiques modernes , l'autèntic fundador del mètode axiomàtic. El 1959 hi va haver un congrés de matemàtics a Royaumont, on el gran matemàtic francés Dieudonné, coautor de Bourbaki, va llançar un crit: "a baix Euclides!"; si bé és obvi que no era cap crítica al geni d'Euclides, sí que era l'inici d'una profunda reforma de l'ensenyament matemàtic, era la fi d'una època mil·lenària.

El sistema axiomàtic d'Euclides i el seu mètode eren insuficients per a una construcció de la geometria independent de l'experiència i de la percepció visual de les formes geomètriques. Euclides feia un ús constant de la intuïció i del que els ulls veuen en les seues demostracions i construccions, i així, per exemple, si una recta passa per un punt interior a una circumferència i per un punt exterior, la recta talla la circumferència; si una circumferència passa per un punt interior i per un punt exterior a una altra circumferència, les dues circumferències es tallen en dos punts, i així es poden citar molts altres exemples. Aquests són fets que podem comprovar visualment en el dibuix sobre el paper, però que és necessari demostrar, i per a la demostració dels quals no n'hi ha prou amb els Elements d'Euclides.

Euclides, encara que platònic, en els seus Elements segueix la línia marcada per Aristòtil de distingir entre axiomes i postulats, els primers són veritats primàries admeses sense demostració, qualsevol que siga la raó per la qual els acceptem, són comuns al raonament lògic, i els segons són solament propis de la geometria. A més a més, fa ús de definicions, de manera que amb aquest bagatge inicial es va desenvolupant tot el saber geomètric. Ja Aristòtil havia indicat que no cal que els postulats siguen vertaders a priori , que la certesa d'aquests es comprova en contrastar amb la realitat els resultats obtinguts. Procle va anar encara més lluny: considera que les matemàtiques són vertaderes només si els supòsits inicials són vertaders i la deducció és correcta. Procle dóna a les matemàtiques un estatus de ciència hipotètica més que no de ciència exacta. Fixem-nos en el fet que l'opinió d'Aristòtil és semblant a la que adoptaran al nostre segle els físics teòrics, i que la de Procle és un avanç de la de Bertrand Russell (1872-1970) que defineix les matemàtiques com la ciència que no sap del que tracta ni si el que diu és veritat o no, amb això fa referència al fet que es parteix de certs postulats que s'admeten com a vertaders, i mitjançant certes operacions conegudes i ben definides, que actuen sobre elements de naturalesa desconeguda, es va obtenint una cadena de teoremes que constitueixen una teoria matemàtica donada. El fet que els elements siguen de naturalesa desconeguda és la raó perquè Russell diu que les matemàtiques no saben del que tracten, i el fet que els teoremes són vertaders únicament i exclusivament si els postulats ho són és la raó perquè diu que ni tan sols saben si el que diuen és veritat. No obstant això, quasi fins al nostre segle s'han considerat axiomes i postulats com a veritats indiscutibles.

Les definicions, els postulats i els axiomes d'Euclides varien lleugerament en les distintes versions dels seus Elements . Seguirem les de Heath o les de Heiberg-Menge més amunt esmentades. A continuació donem algunes definicions:
1. Un punt és allò que no té parts.
2. Una línia és una longitud sense amplària.
4. La recta és la línia que es troba igualment disposada respecte a tots els seus punts
5. Una superfície només posseeix longitud i amplària.
7. El pla és una superfície que es troba igualment disposada respecte a totes les seues rectes.
15. Un cercle és una figura plana rodejada per una línia (la circumferència) tal que totes les rectes que incideixen sobre ella des d'un cert punt interior a la figura són iguals entre si.
16. Aquest punt es denomina centre del cercle.
23. Les rectes paral·leles són les que, estant en el mateix pla, no es troben quan es prolonguen indefinidament en ambdues direccions.

Els cinc postulats són:
I. És possible traçar una recta des de qualsevol punt a qualsevol altre.
II. És possible prolongar indefinidament qualsevol recta.
Una versió distinta del postulat II s'obté substituint en la definició anterior "indefinidament" per "contínuament".
III. Es pot traçar un cercle amb qualsevol centre i radi arbitrari.
Una versió distinta del postulat III s'obté substituint en la definició anterior "arbitrari" per "de qualsevol distància".
IV. Tots els angles rectes són iguals.
V. Si una recta que talla dues altres rectes forma angles interns del mateix costat de la secant, la suma dels quals és més petita que dos angles rectes, aquelles dues, prolongades cap a aquest costat, es troben.
Aquest és el famós postulat de les paral·leles, que de vegades s'ha considerat un axioma, l'axioma XI. Aquest postulat de les paral·leles equival a la proposició XXXI dels Elements , que afirma "per un punt donat es pot traçar una sola recta paral·lela a una recta donada". Hi ha autors que han pres la proposició XXXI com el V postulat, com ara Playfair.

Entre els axiomes, en citarem dos:
VII. Coses que es poden superposar són iguals.
IX. Dues rectes no poden contenir espai.

Les definicions han sigut molt criticades, entre altres raons perquè algunes operen amb conceptes que al seu torn haurien de ser definits i n'hi ha d'altres que no s'empren en la demostració dels teoremes i per tant són inútils i es poden suprimir.

Les definicions 15 i 16, com també la de les esferes, no es compleixen en alguns casos (el centre pot ser exterior al cercle o a l'esfera) com he trobat en les meues investigacions sobre geometria euclidiana en el pla o en espais que no són simplement connexos. Vegeu les figures.

Els postulats i axiomes, llevat del postulat IV, es consideren necessaris, però s'estimen insuficients perquè no poden demostrar frases o proposicions que s'usen en el text, com per exemple "un punt és interior o exterior a un cercle", "dos punts es troben o no en el mateix semiplà dels dos en què una recta divideix un pla". Per tal d'entendre aquestes proposicions cal recórrer al dibuix i a la visió de les figures geomètriques.

L'axioma VII empra el verb "superposar" per tal de demostrar la igualtat, però la realització d'aquesta operació requereix l'ús dels moviments i també ha sigut criticat. Arquimedes (285?-212) que a més a més d'un gran matemàtic també va ser un físic matemàtic, el principi que duu el seu nom és la base de la hidrostàtica, va completar els postulats d'Euclides amb altres cinc postulats, dels quals a continuació en donem tres:
I. Entre totes les línies amb extrems comuns la recta és la més curta.
II. Dues línies qualssevol que tinguen els mateixos extrems, que es troben en un mateix pla i que no siguen iguals, si totes dues són convexes i una d'elles és continguda per l'altra i per la recta que uneix els extrems, la continguda és més petita que la que conté.
V. De dues línies, superfícies o cossos desiguals, la major és més petita que la magnitud que s'obté si es repeteix la menor un nombre adequat de vegades.

Aquest últim axioma és importantíssim i ha passat a la història amb el nom d'axioma d'Arquimedes i els conjunts per als quals és vàlid s'anomenen arquimedians.

L'axioma II i el III i IV, que són una extensió del II, del pla a l'espai depenen de la definició de distància; si s'adopta l'euclidiana, són proposicions que es poden demostrar, i si no s'adopta la distància euclidiana, segons siga aquesta distància, poden no ser vertaders.

Arquimedes va donar també la llei de la palanca i va dir: "doneu-me un punt de suport i alçaré l'univers" frase que ha tingut èxit i així Descartes (1596-1650) va dir "doneu-me extensió i moviment i construiré l'univers". Eddington (1882-1944) l'astrofísic i el matemàtic de la física relativista va dir "doneu-me relacions i construiré l'univers".

A pesar de les mancances i deficiències i dels retocs fets per alguns autors, l'axiomàtica d'Euclides ha durat fins a final del segle XIX en què Hilbert (1862-1943) va establir la seua, que analitzarem més avant. Legendre (1752-1833) va escriure els seus Elements de geometria , que tant van impressionar Galois, el 1794, llibre que va tenir moltes edicions augmentades i corregides fins al 1823. En l'exposició axiomàtica de la geometria segueix la línia euclidiana amb la definició de recta d'Arquimedes. Reproduirem algunes de les primeres frases del seu llibre que són definicions:
1. L'objecte de la ciència de la geometria és la mesura de l'espai. L'espai té tres dimensions: longitud, amplària i alçària.
2. Una línia té longitud però no amplària. Els extrems d'una línia s'anomenen punts. El punt no té extensió.
3. Una línia recta és el camí més curt entre dos punts.

Més endavant afirma "un axioma és una proposició que és evident per si mateixa" i "un teorema és una veritat que es torna evident per mitjà de raonaments anomenats demostració".
Utilitza com a axiomes, entre d'altres:
4. Només hi ha una recta que uneix dos punts.
5. Dues rectes, superfícies o sòlids són iguals si, quan l'un es posa sobre l'altre, coincideixen en totes les seues dimensions.

El canvi important en la forma de veure les coses sorgeix amb l'axiomàtica de Hilbert, en què la geometria es converteix en una construcció intel·lectual independent, estudiada per ella mateixa i no per les seues aplicacions; deixa de ser la tècnica dels agrimensors. Hilbert indica que els seus axiomes estan construïts sobre tres nocions no definides de punt, recta i pla, i que aquests noms són totalment arbitraris, que ell podria haver anomenat "gots de cervesa, cadires i taules". Comparem aquesta opinió de Hilbert, que em sembla que queda dins de la definició de matemàtiques de Russell, amb la definició de geometria de Legendre.

Vistes les opinions d'Euclides, Arquimedes, Legendre i Hilbert, encara que més endavant analitzarem aquesta darrera, podem fer-nos les preguntes següents: què és la geometria?, on és la veritat geomètrica?

És obvi que la geometria és una part de la matemàtica pura, no li és aplicable el mètode experimental, la qual cosa l'allunya de la física, potser d'ací a uns quants anys el progrés dels ordinadors permeta una investigació programada de la geometria, que és el que més s'aproximaria a l'experimentació. D'altra banda és també obvi que les construccions geomètriques es poden dibuixar sobre el paper i que des del descobriment de la geometria descriptiva per Monge (1746-1818), no solament es poden representar sobre el paper les relatives al pla, sinó també les de l'espai, i si bé no podem deduir teoremes dels dibuixos, per contra sí que serveixen per a comprovar la veracitat dels teoremes; i no són només el regle (graduat o no), el compàs, el semicercle graduat i els altres instruments de dibuix els que es poden emprar, sinó que també hi ha altres instruments mecànics, com els planímetres que serveixen per a mesurar àrees. La geometria descriu físicament l'espai i el mesura, serveix de base per a l'explicació dels fenòmens físics, fins al punt que si l'univers en què vivim no estiguera conformat segons el que especifica la geometria euclidiana, la fenomenologia del món físic seria molt distinta de com és, la veritat física depén de la veritat geomètrica. S'ha dit que si els geòmetres no hagueren descobert el nombre p, l'haurien descobert els electricistes.

En la història de la ciència hi ha molts exemples que sobre una base falsa s'ha construït una teoria certa o que almenys ha explicat el que observem i vivim. Així, per exemple, sobre el sistema geocèntric de Ptolemeu, mitjançant un sofisticat i complex conjunt d'epicicles i d'excèntriques s'han pogut explicar els fenòmens observats i calculats pels astrònoms. Carnot (fill) va fer les seues investigacions que van conduir al famós cicle i a la fundació de la termodinàmica sobre la creença falsa en el calòric. Ampère i Faraday van construir l'electromagnetisme sobre la creença falsa de l'electricitat com un fluid de naturalesa desconeguda.

En la mateixa direcció, en més de dos mil anys des d'Euclides fins a Hilbert, a pesar d'usar una base defectuosa i insuficient, i un rigor a vegades dubtós en les demostracions, el coneixement geomètric ha assolit un desenvolupament extraordinari, mai no ha sigut contradit pel dibuix, les màquines i les construccions, ni per la descripció i l'ús del món físic en què vivim. Sempre el talent i la intuïció dels geòmetres ha suplit les errades i les deficiències del sistema euclidià. Es pot dir que la revolució geomètrica de Hilbert ha fet més per l'honor de l'esperit humà que per la mateixa geometria, entenent l'honor de l'esperit humà en el sentit de la cèlebre carta del 2 de juliol de 1830 de Jacobi a Legendre sobre Fourier, en la qual afirmava que "una qüestió sobre nombres val tant com una qüestió sobre el sistema del món".

El 1972 en una conferència de terminologia científica a l'acadèmia della Crusca de Florència, publicada en la revista de l'Acadèmia Toscana de les Ciències i les Lletres de la Colombaria, analitzava la dificultat de definir; deia que s'havien de cercar definicions clares i distintes de les paraules científiques en el sentit cartesià. Com ja havia dit en ocasions anteriors (vegeu la bibliografia) aquestes dues qualitats que Descartes atribuïa a les idees: claredat i distinció, no són al meu parer qualitats independents, és a dir que no es poden millorar indefinidament, sinó que per contra són qualitats complementàries en el sentit de Bohr i de l'escola de Copenhaguen de la mecànica quàntica. A partir de certs límits, com més clara es torna una idea, menys distinta se'ns apareix i recíprocament. Per a mi les idees són més clares com més familiars ens són les paraules que emprem per a expressar-les, i les idees són més distintes com més susceptibles són de ser interpretades matemàticament.

Analitzarem les definicions, els postulats i els axiomes d'Euclides. En primer lloc observem que Euclides defineix objectes geomètrics, proposicions i operacions que ens són familiars en la vida quotidiana, són idealitzacions d'una cosa que veiem. Observem que la definició de punt és pràcticament la mateixa que la de Legendre; aquesta definició ha sigut molt criticada i es considera preferible deixar indefinit el punt i definir les seues relacions amb altres punts i amb altres objectes indefinits, com ho són les rectes i els plans (Hilbert). Tanmateix el que Euclides diu del punt és veritat: si se suprimeix un punt d'una ruta la longitud de la recta no disminueix, però se n'ha modificat profundament la naturalesa topològica, aquesta ha deixat de ser simplement connexa.

Euclides és posterior a Demòcrit (470?-380?), per tant podia haver definit els punts com els àtoms de l'espai. En la matemàtica moderna, en la teoria de conjunts i en els espais abstractes, els punts o elements són els components atòmics dels espais; així com un conjunt té parts (els seus subconjunts), un punt no té parts. El fet de deixar indefinit el punt és una pèrdua de riquesa científica, perquè no sols hi ha punts geomètrics sinó que també hi ha punts físics; el punt material base de la mecànica racional és un punt geomètric dotat de massa; en l'electricitat les càrregues elèctriques puntuals són punts geomètrics amb càrregues elèctriques; els dipols són punts geomètrics sense càrrega elèctrica, però amb un moment elèctric, s'obtenen com a límits d'un procés dinàmic en el qual dues càrregues elèctriques iguals però de signes contraris es van aproximant, de manera que les seues càrregues elèctriques van augmentant, però roman constant el producte de la càrrega elèctrica per la distància entre els punts (el moment elèctric), fins arribar a confondre's els dos punts en un de sol que no tindria càrrega (perquè té dues càrregues iguals infinites però de signe contrari), que tampoc no tindria extensió, l'únic que el punt tindria és un moment elèctric. El mateix es pot dir dels dipols magnètics, i igual que en el cas dels dipols, dues superfícies iguals amb pols magnètics puntuals iguals i oposats que s'aproximen fins que es confonen en una de sola, de manera que el moment magnètic puntual integrat al llarg de la superfície és finit, es transforma en una fulla magnètica, objecte físic molt important que dóna origen a la teoria del potencial de doble estrat, essencial en la física matemàtica.

Quan es diu que un punt no té parts o que no té extensió, s'està transformant en estàtic un procés dinàmic que consisteix en un segment rectilini que es va fent cada vegada més menut, es va esvaint fins que desapareix i aleshores el resultat final d'aquest procés és el punt. Ens recorda el passatge d' Alícia al país de les meravelles del gat que somriu, que va esvaint-se fins que esdevé un somriure sense gat, cosa que Alícia no havia vist mai.

En la definició 4 de recta i en els postulats I i II s'està pensant en la línia que tracem en un paper amb l'ajuda d'un regle, que pot prolongar-se tot el que es vulga i que no deixa cap forat al llarg d'aquesta, que és la percepció visual de la continuïtat. Quan es diu que "es troba igualment disposada respecte a tots els seus punts", es vol dir que no hi ha punts privilegiats, s'està reconeixent implícitament la igualtat de tots els punts de la recta. Només la recta i la circumferència gaudeixen d'aquesta propietat, però les definicions 4 i 15 les distingeixen sense confusió. També la percepció visual ens indica que dos punts qualssevol poden unir-se per una sola recta.

Fins que no apareixen els models euclidians de geometries no euclidianes, no s'està en condicions de distingir entre dues qualitats de la recta que són l'extensió i la longitud. La primera és la propietat que té la recta de ser el suport de punts, i la segona és donada per la distància entre dos punts. Avui podem dir que la recta euclidiana té extensió i longitud infinites; la recta hiperbòlica té extensió finita i longitud infinita, ambdues són obertes; la recta el·líptica té longitud finita i extensió finita o infinita segons el model, és tancada.

Quan es diu que la recta no té amplària, es vol dir que si d'una banda plana se suprimeix una recta paral·lela a les vores de la banda, continua tenint la mateixa amplària. Igual si se'n suprimeix un segment rectilini, però la topologia ha canviat, la banda ha deixat de ser simplement connexa. En dir que "es trobe igualment disposat respecte a totes les seues rectes", es vol dir que no hi ha rectes privilegiades, es proclama la igualtat de totes les rectes del pla. El pla comparteix aquesta propietat amb l'esfera. El que s'ha dit de les rectes euclidianes, el·líptiques i hiperbòliques es pot dir dels plans.

En definir el cercle, definició 15 i postulat III, s'està visualitzant el que es pot dibuixar sobre un paper amb un compàs l'obertura del qual pot modificar-se. Però s'han donat dues versions diferents d'aquest postulat, en una es diu "radi arbitrari" i en l'altra es diu "radi de qualsevol distància" que són molt distintes, la primera és més general, la segona només val per a un espai mètric, és més restringida.

Amb aquesta definició de cercle es defineix una convergència per a les successions de punts del pla, però no una topologia. Per a definir una topologia seria necessari un altre postulat:
III bis. Per a tot cercle, en tot punt interior a aquest cercle es pot traçar un altre cercle, el centre del qual siga aquest punt, i tot els punts del qual siguen interiors al primer cercle.

Un conjunt obert seria per tant aquell en el qual en tot punt d'aquest com a centre es puga traçar un cercle contingut en el conjunt. Els cercles serien conjunts oberts (exclosa la circumferència).

Proveïts de regle i compàs, però usant el regle per a traçar rectes, no per a mesurar-les o transportar-les, es poden fer moltes construccions geomètriques, però ja els grecs van adonar-se que moltes d'altres no poden fer-se, com són per exemple la duplicació del cub (calcular un cub el volum del qual siga el doble d'un altre), la trisecció de l'angle (dividir un angle en tres parts iguals), la quadratura del cercle (construir un quadrat l'àrea del qual siga igual a la d'un cercle donat). Aquest darrer és el més important; l'any 1882 Lindemann va demostrar que era impossible en demostrar que el nombre p és transcendent. Els grecs van utilitzar instruments mecànics per a fer construccions geomètriques.

Mitjançant un moviment un segment rectilini es pot dur a la recta suport d'un altre segment de manera que un extrem del primer coincidisca amb un extrem del segon, i d'aquesta manera comparar-los de manera que formen un conjunt totalment ordenat que és un grup additiu perquè els segments colineals es poden sumar i restar, formen un conjunt dens, és a dir que donats dos segments, sempre n'hi ha un que és més petit que un dels dos anteriors i més gran que l'altre; no existeix un últim element, perquè per gran que siga un segment n'hi ha un altre de més gran. En ser dens es pot transformar en continu completant-lo amb els talls de Dedekind.

Multiplicar un segment per un nombre natural n és sumar n vegades aquest. Multiplicar-lo per -1 és canviar-lo d'orientació. Dividir un segment per un nombre natural n és calcular un altre segment que sumat n vegades done l'anterior. Això últim és una definició l'existència de la qual s'ha de provar; es pot fer emprant les propietats dels triangles semblants que tenen un angle comú.

Una vegada definides la multiplicació i la divisió d'un segment per un nombre enter, queda automàticament definida la multiplicació per un nombre racional. Com que el grup de segments és continu, una vegada definida la multiplicació per un nombre racional, es pot definir la multiplicació per un nombre real; si es postula que el grup dels segments és arquimedià, cosa que es fa mitjançant talls de Dedekind. Resulta que el conjunt dels segments colineals forma un espai vectorial sobre el cos dels nombres reals. Els segments que resulten de multiplicar un segment per un nombre racional qualsevol s'anomenen commensurables, i si és per un nombre irracional s'anomenen incommensurables.

De manera recíproca, donats dos segments qualssevol, sempre un d'aquests és el producte de l'altre per un nombre real, i aquest darrer és el producte del primer pel nombre real invers de l'anterior. Això resulta de la teoria de les proporcions, de les funcions trigonomètriques, de les propietats dels triangles semblants que tenen un angle comú, de la proporcionalitat entre els costats d'un triangle i els sinus dels angles oposats. Es té que el quocient de dos segments és un nombre real, que és aquell pel qual s'ha de multiplicar el denominador per a obtenir el numerador. Vegeu la bibliografia.

Els grecs sabien que 2œ és el quocient de dividir la diagonal pel costat del quadrat i que p és el quocient de dividir la longitud de la circumferència pel diàmetre. Leonardo da Vinci mesurava la longitud d'una circumferència mesurant el recorregut sobre el terra d'una roda que rodava sobre aquest, quan feia una volta completa. Omar Jayyam (1048?-1122) i Nasîr-Eddîn (1201-1274) tenien ja una idea molt clara que la raó de dues magnituds, commensurables o no, és un nombre. El literat àrab modern Amin Maalouf conta en Samarcanda sobre el gran poeta i savi persa Omar Jayyam que en el seu tractat d'àlgebra empra la paraula àrab shay , que significa cosa, per a designar la incògnita; i que els àrabs hispans en lloc de shay escrivien xay , cosa que ha donat origen a l'ús abreviat de la x per a designar la incògnita.

A pesar que es diu que Èudox de Cnidos va emprar l'axioma d'Arquimedes (el V) com un lema, Euclides no el va enunciar de manera explícita, però sí que va fer-ne un ús implícit, i és que l'existència de les paral·leles implica l'axioma d'Arquimedes, i sense axioma d'Arquimedes no hi ha paral·leles, almenys al meu parer. L'axioma d'Arquimedes no es dedueix dels postulats d'Euclides i de les propietats del grup de segments, però sí que es pot demostrar a partir de l'existència de paral·leles i de la proporcionalitat entre els costats d'un triangle i els sinus dels angles oposats, perquè d'això s'infereix que el producte d'un segment per un nombre natural variable arriba a ser més gran que qualsevol segment per gran que siga.

De les propietats anteriors del grup additiu dels segments se segueix una definició de punt: és l'element neutre de l'addició de segments.

Les operacions amb segments que hem exposat abans es poden fer sense necessitat de definir una unitat, però les que definirem ara requereixen definir una unitat que pot ser qualsevol segment escollit arbitràriament. Aquestes són el producte de segments, les potències enteres (positives i negatives), les arrels quadrades i les potències semienteres.

La multiplicació de segments duu a la noció d'àrea, però també d'altres magnituds com per exemple els moments d'inèrcia que encara que introdueixen una altra magnitud, que és la massa, si són cossos homogenis (de la mateixa densitat) es pot prescindir de la massa i es comporten com a magnituds geomètriques. També els moments de vectors són productes de segments, i com que les forces i les velocitats tenen caràcter vectorial, els moments de les forces i els moments cinètics es representen per productes de segments. També les sis coordenades d'una recta (superabundants, perquè només n'hi ha quatre d'independents) que s'usen en la geometria reglada, tres d'aquestes són els components d'un vector, són segments, i les altres tres són els components del moment d'un vector, són productes de dos segments.

Per a la multiplicació de segments i per a les potències enteres es poden emprar les propietats dels triangles semblants que tenen un angle comú, o la propietat que té l'altura perpendicular a la hipotenusa de ser mitjana geomètrica de les projeccions dels dos catets sobre la hipotenusa; però per a les arrels quadrades només l'última. Vegeu la bibliografia.

Escollit un segment arbitrari com a unitat, es pot definir una norma (longitud) sobre l'espai vectorial dels segments (com a vectors) igual al valor absolut del nombre real quocient del segment en dividir-lo per la unitat. L'espai vectorial dels segments és normat i els punts de l'espai euclidià formen un espai mètric, sent la distància entre dos punts igual a la norma del segment que uneix aquests punts. En definir la multiplicació i la divisió de segments queda definida una àlgebra normada en l'espai vectorial normat dels segments. Vegeu la bibliografia.

Al segle XVII es produeix una revolució en la geometria en crear Descartes (1596-1650) la geometria analítica, que aplica els mètodes de l'àlgebra i de l'anàlisi a la geometria. Des d'aleshores hi ha clarament distingibles, encara que de vegades poden actuar de manera conjunta, dos mètodes de fer progressar la geometria: l'analític (el nou) i el sintètic, que no utilitza el càlcul. L'ús de l'anàlisi fa més rica la geometria perquè hi introdueix els punts impropis (punts de l'infinit) que es troben tots sobre la mateixa recta, la recta impròpia (la de l'infinit), per tal de poder manejar-los s'han d'utilitzar coordenades cartesianes homogènies. S'hi introdueixen també figures imaginàries, per exemple les interseccions d'una circumferència i una recta exterior (no secant) són dos punts imaginaris. Dues circumferències qualssevol es tallen en dos punts reals, en un punt real doble (el de contacte) si són tangents o en dos punts imaginaris si són exteriors. Des d'un punt interior a una circumferència es poden traçar dues rectes imaginàries tangents a la circumferència; si aquest punt és el centre, les tangents són les rectes isòtropes, perpendiculars a si mateixes i més concretament que formen amb si mateixes un angle indeterminat. Totes les circumferències tallen la recta impròpia en dos punts fixos imaginaris que són els punts cíclics; les rectes que els uneixen amb el centre de la circumferència són les rectes isòtropes. Es defineixen circumferències i el·lipses imaginàries, que tenen aplicacions físiques.

Augmenta el grau d'abstracció de la geometria perquè els elements imaginaris no són visibles ni es poden dibuixar sobre el paper, però s'hi pot operar amb la mateixa seguretat que amb els reals i obtenir noves transformacions geomètriques i noves propietats i teoremes, de manera que es passa del real a l'imaginari i viceversa. Allò que els sentits no perceben, ho percep la intel·ligència. Una altra conseqüència molt important de la geometria analítica és l'accés a l'estudi dels espais de n dimensions (n>3).

El concepte de circumferència i d'esfera es generalitza sense dificultat a més de tres dimensions i s'obtenen fórmules integrals que donen l'àrea i el volum d'aquestes hiperesferes. Però la generalització també pot fer-se en sentit descendent i així he definit el que he anomenat bipunt (els dos extrems d'un segment). He estés les nocions d'àrea i de volum de la hiperesfera al bipunt i he obtingut el número 2 i la longitud del segment. Així mateix les he esteses al punt (circumferència d'una sola dimensió) i he obtingut per al volum el número 1 i per a l'àrea la funció singular delta de Dirac.

Hi ha vegades que un canvi de definició d'una figura o d'una transformació geomètrica comporta una generalització i l'obtenció de noves propietats. Així, per exemple, dues circumferències s'anomenen ortogonals si es tallen en angle recte, però si una d'aquestes és real i l'altra és imaginària (de centre real i radi imaginari) l'angle amb el qual es tallen no està definit, però es pot estendre la definició d'ortogonalitat anterior per la que li és equivalent segons la qual el quadrat de la distància dels seus centres és igual a la suma dels quadrats dels seus radis (el quadrat del radi d'una circumferència imaginària és negatiu) i aleshores, si existeixen dues circumferències, l'una real i l'altra imaginària que són ortogonals, el que no existeix són dues circumferències imaginàries ortogonals.

Dues circumferències, l'una real i l'altra imaginària, del mateix centre, són ortogonals si els valors absoluts dels radis són iguals, perquè la distància dels seus centres és nul·la. Amb aquesta definició d'ortogonalitat són ortogonals dos bipunts que formen un quatern harmònic. Una circumferència de radi nul és un punt i, amb la definició anterior d'ortogonalitat, tot punt d'una circumferència és una circumferència de radi nul ortogonal a l'anterior. Però per tal d'admetre sense contradicció aquesta proposició cal considerar la circumferència de radi nul com el límit d'una circumferència el radi de la qual tendeix a zero, de manera que aquesta circumferència és una circumferència tangent a un diàmetre de l'anterior en un dels extrems, per tant que té el seu centre sobre la tangent a l'anterior en l'extrem del diàmetre i el centre de la qual s'aproxima al llarg de la tangent indefinidament al punt de contacte (l'extrem del diàmetre) fins que es confonen amb ell. En aquest cas una circumferència de radi nul no és un concepte estàtic sinó que és el resultat límit del procés dinàmic descrit abans. Les circumferències de radi nul i del mateix centre són ortogonals a si mateixes (són isòtropes).

He definit la raó doble de dues circumferències com la raó doble dels quatre punts d'intersecció de les dues circumferències amb el seu diàmetre comú, la qual és igual a -1 si les dues circumferències són ortogonals. Aquesta definició generalitza el concepte d'angle a dues circumferències reals que no es tallen i a circumferències reals i imaginàries. Aquesta raó doble és també la raó doble de les quatre interseccions de les dues circumferències amb una circumferència qualsevol que siga ortogonal a les dues anteriors. La raó doble degenera en una raó simple de tres punts si una circumferència degenera en una recta. Generalitza el concepte d'angle a bipunts i és extensible a esferes. És una nova definició projectiva d'angle. Vegeu la bibliografia.

Es pot aplicar un principi d'inducció completa en la geometria euclidiana de n dimensions i demostrar que si un teorema o una construcció geomètrica és vàlid en un espai euclidià de n-1 dimensions, és vàlid per a un de n dimensions. Així, he pogut demostrar (vegeu la bibliografia) que:
1. El nombre màxim d'esferes ortogonals dos a dos en un espai euclidià de n dimensions és n+2, de la qual una és imaginària. Resultat vàlid també per a la recta.
2. Els centres de les n+1 esferes reals ortogonals són els vèrtexs d'un n+1-edre ortocèntric d'ortocentre interior (l'ortocentre és el punt en el qual les altures es tallen).
3. El centre de l'esfera imaginària ortogonal a les anteriors és l'ortocentre.
4. Una cara qualsevol d'aquest n+1-edre és un n-edre de l'espai euclidià de n-1 dimensions, també ortocèntric, en el qual els n vèrtexs són els centres de n esferes reals, i l'ortocentre és el centre d'una esfera imaginària, ortogonals dos a dos.
5. L'esfera secció per la dita cara de l'esfera real el centre de la qual és el vèrtex oposat del n+1-edre, és una esfera imaginària, la mateixa que l'esfera secció per l'anterior cara de l'esfera imaginària el centre de la qual és l'ortocentre del n+1-edre.

Es pot continuar aquest procés de pas d'un n+1-edre a un n-edre fins arribar al tetraedre, el triangle i la recta, figures geomètriques que ens són més familiars.

Els resultats anteriors permeten construir un n+1-edre ortocèntric en un espai euclidià de n dimensions. Així com tots els triangles són ortocèntrics, no succeeix el mateix des del tetraedre cap amunt. En un n+1-edre ortocèntric, els vèrtexs i l'ortocentre són n+2 punts, dels quals n+1 qualssevol poden considerar-se com a vèrtexs i el punt restant és l'ortocentre, de manera que hi ha n+2 distints n+1-edres ortocèntrics obtinguts tots a partir d'un qualsevol d'aquests, però de tots aquests només n'hi ha un que tinga interior l'ortocentre.

El V postulat d'Euclides, el de les paral·leles, té una història singular, el mateix Euclides i els seus primers comentaristes van dubtar de si es tractava d'un postulat o si es podia considerar una proposició demostrable, per la qual cosa van intentar evitar, si era possible, en les seues demostracions l'ús del V postulat i per aquesta raó tots els teoremes i les construccions que no requereixen l'ús del V postulat formen la geometria absoluta, mentre que els altres formen la geometria euclidiana pròpiament dita.

Les geometries no euclidianes clàssiques parteixen de la negació del V postulat i n'hi ha dues, una de les quals és la hiperbòlica, en què per un punt es poden traçar dues paral·leles a una recta donada, i l'el·líptica, en què no existeixen rectes paral·leles. Tota teoria científica té una història i una prehistòria. La prehistòria de la geometria no euclidiana naix al segle XVIII amb Saccheri i Lambert i la història naix al segle XIX amb Lobatschewski i Bolyai.

Abans del segle XVIII hi ha intents fallits de demostrar el V postulat, alguns dels quals són molt enginyosos. És Saccheri (1667-1733) qui en la seua lògica demostrativa i en Euclides ab omnis naevo vindicatus publicat l'any de la seua mort, utilitza una figura que no existeix en la geometria euclidiana, però sí en la no euclidiana, que és el quadrilàter birectangle isòsceles (en la geometria euclidiana seria forçosament un rectangle), i fa la hipòtesi que els dos angles no rectes, que són iguals, siguen un angle agut, recte o obtús. Entre altres conclusions importants afirma que segons es verifique la hipòtesi de l'angle agut, recte o obtús, la suma dels angles d'un triangle serà menys, igual o més gran que dos angles rectes. Com és natural, no aconsegueix demostrar que el V postulat és vertader, però la seua obra és molt notable perquè si bé considera que la hipòtesi de l'angle obtús és falsa (cosa que no és veritat), no descobreix contradiccions en la hipòtesi de l'angle agut i la nega perquè la considera contrària a la naturalesa de la línia recta. En no descobrir contradiccions en la hipòtesi de l'angle agut, s'estableix el dubte molt raonable que el V postulat siga indemostrable i que es puga construir una geometria consistent negant-lo. Saccheri va ser molt difós al segle XVIII, però després va caure en l'oblit, fins que Beltrami el 1889 en una nota en els Rendiconti de l'Acadèmia de Lincei, titulada "Un precursor italià de Legendre i Lobatschewski" el va tornar a col·locar al seu lloc, i va aconseguir que la seua obra fóra traduïda a l'anglés (1894), a l'alemany (1895) i a l'italià (1904).

Lambert (1728-1777) en la seua Theorie des Parallellinien (1766), publicada el 1786, després de morir, utilitza una figura que és el quadrilàter trirectangle, que té tres angles rectes i el quart a priori desconegut, el qual pot ser agut, recte o obtús. La hipòtesi de l'angle recte condueix a la geometria euclidiana, la de l'angle obtús la rebutja (equivocadament) i en la de l'angle agut obté diverses conclusions importants. Des de Saccheri i Lambert, els precursors de la geometria no euclidiana, fins als fundadors, Lobatschewski (1829) i Bolyai (1832) transcorre entre mig segle i un segle. En aquest temps es continua pensant i escrivint sobre aquesta matèria: D'Alambert (1736-1813), Legendre, Schweikart (1780-1859), Taurinus (1794-1874) amb importants resultats analítics. De la relació de Gauss amb la geometria no euclidiana, me n'he ocupat en altres ocasions.

Indubtablement és Lobatschewski el vertader creador de la geometria no euclidiana i qui per primera vegada li va donar un gran desenvolupament. L'11 de febrer de 1826 va llegir una memòria a la universitat de Kazan, on per primera vegada fa una exposició de la seua nova geometria. Aquesta memòria no es va publicar i el manuscrit s'ha perdut. El 1829 va publicar una memòria en El Missatger de Kazan , que és la primera obra llarga i important de la geometria no euclidiana, que ell va anomenar imaginària i que avui anomenem hiperbòlica. Durant els anys trenta va continuar publicant sobre aquesta matèria i el 1840 va publicar en alemany les seues Investigacions geomètriques sobre la teoria de les paral·leles . La seua última obra, Pangeometria , publicada l'any 1855 en rus i en francés, conté una exposició molt completa de la seua nova geometria.

Bolyai (1802-1860) independentment de Lobatschwski, va arribar a la mateixa nova geometria; els seus treballs van ser publicats en forma d'apèndix en el primer volum d'un llibre de son pare, Wolfgang, titulat Tentamen... el 1832.

Quan la geometria euclidiana es va descobrir no va cridar massa l'atenció, a pesar de la seua gran importància i de la novetat i l'originalitat que tenia, que anava en contra de la nostra intuïció i de l'experiència física. A partir de la dècada dels seixanta del segle XIX es desperta un gran interés per aquesta geometria i se n'aprofundeix l'estudi seguint dues grans direccions: la de la geometria diferencial i la de la projectiva. Gauss havia aprofundit molt en l'estudi de la geometria diferencial, i havia assenyalat que tota superfície té una geometria intrínseca, que li és pròpia, independent de la geometria de l'espai en què es troba immersa; és notable la seua obra de 1827 Investigacions generals sobre superfícies corbes . Un pas decisiu en aquesta direcció és el que va fer Riemann, el qual a partir del seu discurs d'habilitació per a la Universitat de Göttingen el 1854 (publicat el 1867) i d'un treball sobre la conducció de la calor presentat a un premi de l'Acadèmia de Ciències de París, que no va guanyar, va desenvolupar la teoria dels espais que duen el seu nom, espais de n dimensions, amb una geometria diferencial pròpia en la qual totes les seues propietats mètriques estan implícites en l'element lineal que és una forma quadràtica homogènia de les diferencials de les coordenades. A partir d'aquesta s'obtenen les geodèsiques, que són la distància més curta entre dos punts, i s'introdueix el concepte de curvatura, que serà molt important per a la relativitat d'Einstein. Aquest concepte de curvatura generalitza el que Gauss havia introduït per a les superfícies.

Hi havia latent el problema de trobar, si existia, una superfície la geometria intrínseca de la qual fóra la del pla de Lobatschewski-Bolyai. Per a això era necessari trobar superfícies que pogueren moure's amb flexió, però sense extensió, sobre elles mateixes, com ho fa un pla, de manera que puga definir-se una igualtat entre figures sobre la superfície, tal que figures iguals es puguen superposar mitjançant un moviment sobre la superfície. Perquè dues superfícies siguen aplicables l'una sobre l'altra, la curvatura de Gauss ha de ser la mateixa en punts homòlegs (aplicats els uns sobre els altres). Minding va demostrar que si la curvatura és constant, la superfície pot moure's lliurement sobre ella mateixa.

Beltrami, en dues memòries publicades el 1868 que es titulen Assaig d'interpretació de la geometria no euclidiana i Teoria dels espais de curvatura constant, va reconéixer que les superfícies de curvatura constant són plans no euclidians; va demostrar que la geometria d'una part, però sols d'una part, del pla de Lobatschewski és la mateixa que la geometria intrínseca de la pseudoesfera, si les longituds i els angles del pla no euclidià es prenen iguals a les longituds i angles de les geodèsiques de la pseudoesfera. Sobre aquesta pot moure's una figura, de manera que corbant-la es pot ajustar a la superfície de la pseudoesfera. És el primer model euclidià de geometria hiperbòlica (de Lobatschewski). La pseudoesfera és una superfície de curvatura constant negativa, és engendrada per la revolució d'una tractriu al voltant de la seua asímptota, la tractriu és una corba per a la qual és constant la longitud de la tangent compresa entre el punt de contacte i l'asímptota; la seua evoluta és una catenària.

En demostrar Beltrami que podia representar-se una part del pla hiperbòlic sobre la pseudoesfera, el problema de si podia representar-se el pla hiperbòlic complet sobre alguna superfície de curvatura constant negativa quedava obert.

Hilbert el 1901 va millorar un resultat anterior de Helmholtz, que havia demostrat que no existeix cap superfície de curvatura negativa constant que puga estendre's en totes direccions, i va demostrar que no existeix cap superfície analítica, regular per totes parts, sense singularitats i de curvatura negativa constant sobre la qual es verifique en la seua integritat el pla de Lobatschewski. La qual cosa dóna una contestació negativa al problema obert al final del paràgraf anterior.

Saccheri i Lambert havien rebutjat la hipòtesi de l'angle agut perquè consideraven la recta infinita. Riemann va substituir aquesta idea per la de recta il·limitada, afirmava que "la propietat de l'espai de ser il·limitat posseeix, doncs, una certesa empírica... si s'atribueix a l'espai una curvatura constant positiva, l'espai serà necessàriament finit". Per a Riemann el postulat que atribueix a una recta una longitud infinita és tan discutible com el postulat de les paral·leles; el que per a ell és indiscutible s l'espai il·limitat. El pla (no euclidià) el·líptic duu avui també el nom de Riemann, en el qual les geodèsiques són tancades, de longitud finita i es tallen totes. La idea d'un univers corb, finit però il·limitat va adquirir gran importància amb la cosmologia relativista.

L'altra línia de pensament que es va seguir per a la investigació de la geometria no euclidiana va ser la de la geometria projectiva.

Els noms de Cayley (1821-1895) i Klein (1848-1925) van associats a aquesta tendència. Aquest darrer el 1871 (encara que publicat el 1874) va distingir entre dues classes de plans el·líptics, que són el doblement el·líptic o esfèric, i el simplement el·líptic. Un model del primer és l'esfera en què dos punts no sempre determinen una recta (si són diametralment oposats) i un model del segon és un hemisferi que porte inclosa la seua frontera (el pla diametral), però en el qual els dos punts diametralment oposats de la frontera han d'identificar-se com un sol punt. Les línies geodèsiques són les semicircumferències dels cercles màxims, que són corbes tancades en identificar-se en un sol punt els seus dos extrems. Les distàncies no euclidianes són els arcs de geodèsiques mesurats euclidianament i els angles coincideixen amb els euclidians.

Beltrami havia reconegut que el pla el·líptic podia representar-se sobre una superfície de curvatura constant positiva i Liebmann el 1899 va demostrar que una superfície analítica, tancada, lliure de singularitats i de curvatura constant positiva necessàriament és una esfera.
Poincaré va donar altres models euclidians de geometries no euclidianes, va utilitzar les propietats del pla hiperbòlic en les seues investigacions sobre les funcions automorfes, fetes entre 1881 i 1884. Les funcions automorfes són funcions de variable complexa, invariants per a les transformacions homogràfiques (de determinant igual a 1), de les quals les funcions trigonomètriques i les el·líptiques són casos particulars. Per a Poincaré el fet de poder construir models euclidians de les geometries el·líptica i hiperbòlica fa que tota contradicció en aquestes arrossegaria una contradicció en la geometria euclidiana, per la qual cosa la consistència de les tres geometries està indissolublement lligada. El V postulat d'Euclides no és vertader ni fals, ja que tant l'afirmació com la negació d'aquest condueixen a geometries distintes, que són coherents i consistents.

Un altre model euclidià de pla el·líptic interessant va ser donat per Klein; és la secció per un pla d'una radiació de rectes i plans, associat a la polaritat absoluta (ortogonal).

Laguerre (1834-1886) el 1853, quan tenia 19 anys, va fer la primera definició projectiva d'angle com a proporcional al logaritme de la raó doble del quatern de rectes format pels costats de l'angle i les rectes isòtropes que passen pel vèrtex de l'angle, és a dir que projecten des d'aquest vèrtex els punts cíclics de Poncelet (l'absolut de Laguerre). Cayley i Klein van generalitzar aquest descobriment de Laguerre i, subordinant la geometria mètrica a la projectiva mitjançant l'ús de formes quadràtiques de les coordenades (que recorden les de Riemann de les diferencials de les coordenades), van definir la distància i l'angle com a magnituds proporcionals a logaritmes de raons dobles, i van substituir els punts cíclics per un nou absolut: una cònica en el pla i una quàdrica en l'espai. De manera que la distància de dos punts és proporcional al logaritme de la raó doble d'un quatern de punts format pels dos punts i les interseccions de la recta que uneix els punts amb l'absolut; així mateix l'angle de dues rectes és proporcional al logaritme de la raó doble d'un quatern de rectes format pels costats de l'angle i les tangents a l'absolut que passen pel vèrtex de l'angle. Vegeu la meua Geometria analítica i projectiva.

A final del segle XIX sorgeix un gran interés pels fonaments de les matemàtiques i en particular de la geometria euclidiana. Pasch (1843-1931) en el seu curs sobre la nova geometria, la primera edició del qual és del 1882 i que va ser reeditat i revisat per Dehn (1878-1952) el 1926, és un pioner en aquesta nova línia de cercar una axiomàtica, i va introduir un nou axioma que duu el seu nom i que s'ha fet cèlebre; afirma "siguen A, B i C tres punts no alineats i siga a qualsevol recta del pla determinat per A, B C, i que no passe per cap d'aquests tres punts. Si a passa per algun punt del segment AB, també ha de passar per algun punt del segment AC o per algun punt del segment BC".

És curiós que l'axioma de Pasch que és tan perceptible, perquè és impossible dibuixar en un paper, qualsevol que siga la seua grandària, un triangle en què no es complisca l'axioma de Pasch, fins i tot en un triangle degenerat en el qual un vèrtex es troba en l'infinit, no s'haja formulat fins a final del segle XIX. En canvi, l'existència de paral·leles i el V postulat d'Euclides es van formular des del principi, encara que per contrastar-lo per la percepció visual es necessitaria un paper de dimensions infinites.

En les meues investigacions sobre geometries euclidianes i no-euclidianes en espais que no siguen simplement connexos (connexió lineal o superficial) he trobat triangles no paschians, en els quals no es compleix l'axioma de Pasch. Vegeu més endavant.

L'obra mestra en aquest camp, encara que no l'única són Els fonaments de la geometria de Hilbert, que es va editar per primera vegada l'any 1899 i després va ser reeditada i revisada diverses vegades fins arribar a la setena edició el 1930. Em referiré a aquesta última edició, en què Hilbert utilitza vint axiomes que divideix en cinc grups: el primer en té vuit, els d'incidència o connexió, que estableixen l'enllaç entre els ens geomètrics bàsics: punts, rectes i plans, que deixa indefinits. El segon grup en té quatre, els d'ordenació, que defineixen el concepte de "trobar-se entre" i ordenen els punts sobre una recta; el quart axioma d'aquest grup és el de Pasch. El tercer grup en té cinc, els de congruència, que defineixen el concepte de moviment i estableix la igualtat o congruència de segments i d'angles, permet el transport i l'addició de segments i d'angles i comprovar-ne la igualtat per superposició, i permet comparar entre si la magnitud dels segments; defineix els angles rectes i la seua igualtat. El quart grup té un sols axioma, que és el de les paral·leles (el V postulat d'Euclides), permet demostrar que la suma dels angles d'un triangle val dos angles rectes, i permet definir i provar l'existència de la circumferència. El cinqué grup té dos axiomes, els de continuïtat, són els d'Arquimedes i el de la plenitud, per a establir una correspondència entre els punts de la recta i els nombres reals, cosa que per a ell demostra la identitat de la seua geometria amb la geometria analítica de Descartes.

En aqust llibre, en l'apèndix III, exposa una axiomàtica del pla hiperbòlic (pla de Lobatschewski-Bolyai) basat en quatre grups d'axiomes. El primer format per tres axiomes, els d'incidència i connexió, que són els tres primers utilitzats per a la geometria euclidiana; suprimeix els cinc axiomes següents, en els quals intervé el pla. El grup segon són els mateixos quatre axiomes del grup segon de la geometria euclidiana, incloent-hi l'axioma de Pasch. El grup tercer també és el mateix de la geometria euclidiana. El grup quart està format per un sols axioma, que substitueix el de les paral·leles, que ell anomena de les rectes secants i no secants que afirma "Siga una recta qualsevol b i un punt A no situat en aquesta, sempre hi ha dues semirectes a1 i a2 que passen per A, que no constitueixen una sola recta i que no tallen la recta b , mentre que tota semirecta que passa per A, situada en l'espai angular format per a1 i a2 talla la recta b ". Els axiomes de continuïtat són necessaris.

El conjunt dels segments hiperbòlics és també continu i arquimedià, però canvia la definició de distància que ja no és la longitud l del segment sinó que és RArg.Th(l/R), en què R és una constant, que és una unitat natural de mesura que existeix en la recta hiperbòlica.

En la recta euclidiana no existeix cap unitat natural de mesura. En l'espai euclidià aquest és únic però hi ha figures semblants; per contra, en l'hiperbòlic no hi ha figures semblants, però sí que hi ha espais semblants, en variar el valor de R. La magnitud -1/R2 és la curvatura constant negativa de l'espai hiperbòlic.

Al segle XVIII es va establir una trigonometria analítica en la qual els angles són els arguments de les funcions trigonomètriques, que s'expressen mitjançant funcions exponencials d'exponent imaginari, cosa que permet estudiar-los a través dels seus desenvolupaments en sèrie de potències i de les seues propietats com a solucions d'equacions diferencials. Aquesta teoria analítica és idèntica a la teoria geomètrica en la qual també pot basar-se la trigonometria. Això no deixa de ser un fet sorprenent del comportament de la natura.
En un grup arquimedià en el qual existeix la divisió per un nombre natural, com a operació inversa de la multiplicació, es demostra que, donats dos elements a i b , en què a és més petit que b , existeix un nombre natural n tal, que b dividit per n és més petit que a , perquè en cas contrari no es compliria l'axioma d'Arquimedes. Propose anomenar aquest teorema de la divisibilitat indefinida. De manera recíproca, si en un grup additiu totalment ordenat, en el qual existeix la divisió, el teorema anterior es compleix, el grup és arquimedià perquè es demostra l'axioma d'Arquimedes com si fóra un teorema.

Els angles són els quocients de dividir els arcs d'una circumferència pel radi, per tant són nombres reals, que són majors o iguals que zero i menors que 2p. Els angles es poden sumar amb una nova definició de suma que és la següent: si la suma ordinària de dos angles és més petita que 2p, es pren la nova suma igual a l'ordinària; si és igual o més gran que 2p, la nova suma es pren igual a la suma ordinària disminuïda en 2p; en el primer cas l'addició és compatible amb la relació d'ordre (dels nombres reals) i en el segon no ho és. Els angles no formen grup, sinó un semigrup amb element neutre per a l'addició i en el qual és vàlida la regla de simplificació que afirma que si a dos angles a i b se'ls suma un mateix angle gamma i s'obtenen dos angles iguals a+gamma i b+gamma, aleshores a és igual a b. Els angles es poden multiplicar i dividir per un nombre natural n . En el conjunt dels angles l'axioma d'Arquimedes no val, però sí el de la divisibilitat indefinida.

Em sembla que qualsevol que siga l'axiomàtica de la geometria euclidiana, ha de conduir a una estructura del conjunt dels angles descrit en els paràgrafs anteriors i del conjunt dels segments a l'estructura descrita en els paràgrafs anteriors a parlar de la geometria analítica.

Crec que l'axiomàtica de la geometria euclidiana ha de ser analítica i aquesta condueix a obtenir pel càlcul el V postulat d'Euclides, l'axioma d'Arquimedes i l'axioma de Pasch. L'he desenvolupada, però no l'he publicada encara.

Quan es diu que el quocient de dos segments és un nombre real, es vol dir que escollit un segment arbitrari e com a unitat, existeix una bijecció entre el conjunt dels segments d i dels nombres reals R tal que al segment e li correspon el número 1 i a qualsevol altre segment r li correspon el nombre real definit pel quocient r/e. El canvi d'unitat en d es fa com el canvi d'escala en un mapa. S'obté dn a partir de d com Rn a partir de R.

Quan es diu que els punts d'una recta D es poden identificar amb els nombres reals (R) es vol dir que existeix una bijecció de D sobre R tal, que a dos punts arbitraris A i B els corresponen els punts 0 i 1, i a qualsevol punt C de D li correspon el nombre real r , definit pel quocient AC/AB, que anomenem abscissa de C; O és l'origen d'abscisses i AB el segment unitat. Vegeu la bibliografia.

En els axiomes (nocions comunes) d'Euclides s'empren paraules que no tenen una significació exacta i precisa, com és el cas d'"afegir o sumar" i de "llevar o restar". Per exemple l'axioma III, que ha sigut emprat per molts altres autors i es continua emprant, afirma que "Si es resten coses iguals a coses iguals, les restes són iguals", doncs bé, aquest axioma val per a segments i angles, en general per a grups additius i semigrups additius en els quals val la regla de simplificació, però l'axioma III no és cert en els semigrups additius en els quals no val la regla de simplificació.

L'espai euclidià habitual E és simplement connex, però hi ha altres models d'espais euclidians que no són simplement connexos, dotats d'una mètrica distinta però equivalent. Un d'aquests és el que he anomenat (vegeu la bibliografia) pla incomplet inversiu PI, que és un pla euclidià desproveït d'un punt P, en el qual els punts són els mateixos que els del pla euclidià (excepte P) i en el qual les rectes són les circumferències i les rectes que passen per P (exclòs aquest punt P). Si s'inverteix aquest pla amb centre en P i potència qualsevol, es transforma en un pla euclidià E, de manera que la distància entre dos punts de PI és igual a la distància euclidiana entre els dos punts inversos quan es pren la unitat com a potència. Els angles són els euclidians.

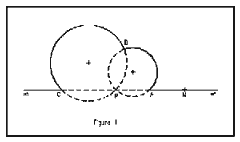
Els triangles estan formats per tres punts qualssevol de PI, que són els vèrtexs, units per "rectes de PI" (arcs de circumferències o parts de rectes que passen per P) que són els costats. El PI té propietats curioses, no és paschià, i s'entén per paschià que hi ha triangles per als quals l'axioma de Pasch no es compleix.

Els triangles no paschians (figura 1) són els que tenen els vèrtexs A i C sobre una recta que passa per P, i estan separats per P; si B és el tercer vèrtex, els costats AB i BC són arcs de circumferències que passen per P, i el tercer costat és la recta APC, exclòs el segment AC. Per tant les rectes que passen per P, que són rectes de PI (excepte les rectes PB i AC) sols tallen un dels costats AB o BC del triangle, que per tant no és paschià.

(fig. 1)

Tots els punts de l'infinit del pla euclidià E s'identifiquen en PI en només un (infinit). Les rectes de PI paral·leles són les circumferències tangents en P i la tangent a elles en P. La distància de qualsevol punt de PI a P val infinit. En la recta AC (figura 1) si es vol anar de A a C o de C a A no es pot fer a través de P, sinó a través de infinit de manera que el punt M "es troba entre A i C" a pesar que en la figura queda fora de AC.

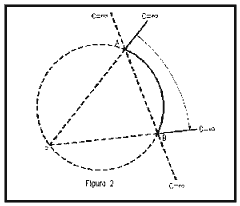
(fig. 2)

Els triangles que tenen els costats que són rectes que passen per P tenen l'estrany dibuix de la figura 2. Un costat AB és l'arc de la circumferència que passa per P i els altres dos costats són la part AC (C=infinit) i BC de les rectes PA i PB, i el punt C, tercer vèrtex del triangle ABC, és l'únic punt de l'infinit de PI.

Les circumferències SIGMA de PI i d (figures 3 i 4) es dibuixen com unes circumferències euclidianes i rectes euclidianes que no passen per P. Si AB és el diàmetre de la circumferència euclidiana (figura 3) SIGMA, si C és el punt P de PI, aleshores el centre de la mateixa circumferència SIGMA del PI és el conjugat harmònic D de C respecte a A i B, que és en el PI el punt mitjà de AB (mentre que el punt mitjà de AB és el centre euclidià de la circumferència euclidiana). Els diàmetres en el PI de SIGMA són els arcs interiors a SIGMA de les circumferències que passen per D i C (punt P del PI). El cercle és l'interior de SIGMA.

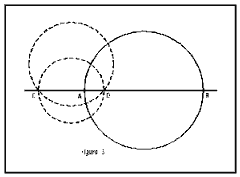
(fig. 3)

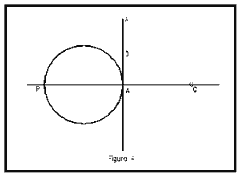
(fig. 4)

Si el punt P del PI (figura 3) és ara el D, interior a SIGMA, aleshores el centre de SIGMA de PI és el punt C exterior a SIGMA i els diàmetres són els arcs exteriors a SIGMA de les circumferències que passen per C i D (ara el punt P del PI). El cercle és l'exterior de SIGMA, C i D i exterior i interior de SIGMA permuten els seus papers.

Hi ha, doncs, casos en què el punt mitjà d'un segment (el conjugat harmònic de P respecte als extrems del segment) queda fora del segment, però equidista dels seus extrems. I també hi ha casos en què el centre d'una circumferència és exterior a aquesta, però equidista d'ella. Això va en contra de la definició 16 de centre d'un cercle d'Euclides, però no contra la definició 15 de circumferència, el que s'ha canviat és la definició de distància.

Una recta euclidiana és també una circumferència d de PI (figura 4), perquè les circumferències de PI són les inverses de les circumferències de E. Les rectes són inverses de les circumferències que passen per P, per tant són circumferències de PI. Donada la circumferència SIGMA de diàmetre PA tangent a AB en A, si prenem com a centre d'inversió P i com a potència d'inversió PA2, la circumferència de diàmetre PA es transforma en la recta AB, que és una circumferència d de PI, el centre de la qual és l'invers del centre de SIGMA, per tant és un punt O, tal que PA=PO i els diàmetres els arcs de les circumferències que passen per P i O continguts en el semiplà a la dreta de AB que és el cercle. Si s'aplica la mètrica de PI per al càlcul de la longitud de d i de l'àrea del cercle (semiplà a la dreta de AB) s'obtenen la longitud i l'àrea de SIGMA. Qualsevol àrea del semiplà a la dreta de AB limitat per dues paral·leles a AB té una àrea finita, la qual cosa va contra l'axioma IX d'Euclides.

Assenyalem com a curiositat que la recta AB en la figura 2 és la circumferència del PI circumscrita al triangle ABC (C=infinit).

En suprimir el punt P del PI en qualsevol circumferència, l'ordenació és com la d'una recta, és a dir, que donats tres punts qualssevol, un d'aquests es troba entre els altres dos, mentre que si no s'haguera suprimit el punt P, qualsevol dels tres punts anteriors es trobaria entre els altres dos.

El que s'ha dit s'estén a qualsevol nombre de dimensions. A partir de tres dimensions en suprimir un punt P, l'espai continua sent simplement connex per a la connexió lineal, però no ho és per a la connexió superficial en el cas de tres dimensions; seria similar al que resulta de suprimir tota una esfera, o al que hi ha a l'interior d'una corona esfèrica.

De la projecció inversa de l'estereogràfica d'una esfera, un pla euclidià E o un pla inversiu PI donen models amb distinta mètrica d'aquestes geometries, en suprimir el centre de projecció de l'esfera. El model inversiu és també l'induït sobre una esfera que passa pel punt P, per l'espai inversiu incomplet.

Les exposicions abstractes de les geometries hiperbòlica i el·líptica no permeten dibuixar sobre el paper les figures i construccions d'aquestes, ni plasmar-les en l'espai. Si observem les figures que hi ha en els textos, com en l'apèndix III d' Els fonaments de la geometria de Hilbert són solament il·lustratives per tal de facilitar la comprensió del raonament, però en si mateixes no tenen contingut, poden ser substituïdes per altres qualssevol; concretament en la que utilitza per a enunciar l'axioma de les rectes secants i no secants, les dues semirectes que utilitza s'uneixen en un punt de retrocés, quan la recta és una corba contínua i diferenciable. L'existència de models euclidians de geometries no euclidianes permet dibuixar sobre el paper propietats i relacions entre els ens no euclidians i utilitzant els mètodes de la geometria descriptiva es poden representar sobre el paper els sòlids no euclidians. Per exemple el càlcul abstracte dels sentits (propietat física de les rectes hiperbòliques) es pot concretar en un càlcul geomètric euclidià concret, que he desenvolupat i aplicat a la cinemàtica de la teoria de la relativitat.

Per a definir un model euclidià d'un espai hiperbòlic o el·líptic cal definir la mètrica lineal (la distància) mitjançant l'element lineal dr, cosa que determina les seues geodèsiques o distàncies més curtes entre dos punts (les rectes no euclidianes), i la mètrica angular, és dir el cosinus (o el sinus) de l'angle de dues geodèsiques que es tallen en un punt; i així mateix si l'espai euclidià suport és tot l'espai euclidià o un subespai, o una superfície euclidiana o part d'aquesta (esfera, pseudoesfera, últimament he utilitzat l'hiperboloide de revolució per a aplicar-lo a la cinemàtica relativista). S'imposa la condició que dos punts determinen una recta; tres punts determinen un pla. El model pot tenir més de tres dimensions.

Ara considerarem alguns d'aquests models sobre els quals he investigat. D'aquests models, n'hi ha que són simplement connexos i n'hi ha que no (siga per a una connexió lineal o superficial). Són models de dues a n dimensions.

En el model H1 del pla hiperbòlic (simplement connex), conegut des de temps antic, les geodèsiques són arcs de circumferències ortogonals a una circumferència fixa SIGMA (inclosos els diàmetres) interiors a aquesta, que actua com a frontera, és el conjunt dels punts a distància infinita. Els centres de les geodèsiques són exteriors a SIGMA. Els angles són els euclidians, i la mètrica dóna una representació conforme de H1 sobre l'espai euclidià. Per tal de definir-los en n dimensions s'ha de substituir la circumferència SIGMA per una esfera de n dimensions. En el cas de tres dimensions, els plans no euclidians són els casquets interiors a l'esfera fixa SIGMA, de les esferes ortogonals, i els cercles dels plans diametrals de SIGMA que es troben sobre SIGMA. Les rectes no euclidianes (les geodèsiques) són les interseccions dels plans no euclidians. He pogut construir una geometria reglada hiperbòlica en la qual les coordenades d'una recta són sis; les tres coordenades cartesianes del centre de la circumferència euclidiana suport de la recta hiperbòlica (a, b, c) i les tres coordenades pluckerianes (u, v, w) del pla diametral en què es troba situada; però d'aquestes sis coordenades, només n'hi ha quatre d'independents, perquè les tres u, v, w són homogènies, poden ser substituïdes per nombres proporcionals, i a més a més existeix una relació bilineal entre les sis coordenades perquè el punt (a,b,c) es troba sobre el pla (u,v,w), que és que la suma dels tres productes ua+vb+wc és igual a zero.

En H1 té un paper molt important la inversió que sol deixar invariant l'espai o transformar-lo en un altre de semblant. Mentre que en l'espai euclidià E hi ha figures semblants, però no hi ha dos espais semblants, per ser únic l'espai; en H1 sí que pot haver-hi espais semblants, hi ha la possibilitat d'una pluralitat de móns, però dins d'un mateix H1 no hi ha figures semblants. Si el radi R de SIGMA tendeix a infinit, H1 tendeix a E; i si R tendeix a zero, H1 tendeix a desaparéixer.

En H1 hi ha figures imaginàries, en el cas del pla hiperbòlic són rectes no euclidianes imaginàries, les circumferències imaginàries ortogonals a SIGMA (els centres de les quals són interiors a SIGMA), cosa que m'ha permés desenvolupar una trigonometria dels triangles imaginaris i dels quadrilàters complets imaginaris, en la qual existeixen rectes reals antiparal·leles respecte a un angle imaginari i rectes imaginàries antiparal·leles respecte a un angle real.

Mitjançant una inversió que deixe invariant SIGMA es pot transformar qualsevol punt A de H1 en el seu centre O, i O es transforma en A. Si considerem la inversió anterior com una transformació de coordenades, H1 té la propietat que he proposat anomenar isotòpica, que consisteix en el fet que a qualsevol observador situat en qualsevol punt A de H1 li sembla veure H1 igual, fins i tot si a O li sembla que A es troba a la seua dreta o damunt, a A li sembla que és O qui es troba a la seua dreta o damunt.

He pogut demostrar que així com en el pla no hi ha circumferències imaginàries ortogonals, per contra en l'espai sí que hi ha circumferències imaginàries i fins i tot de radi zero ortogonals a una circumferència imaginària.

Mitjançant una inversió de centre O (centre de SIGMA) i potència R2 (R radi de SIGMA) el model hiperbòlic H1 es transforma en el H2 , que no és simplement connex, del qual no poden coexistir més d'un, a diferència del que succeïa amb H1 . Donats un H1 i un H2 amb la mateixa frontera SIGMA, que els separa, existeix una bijecció entre tots dos, en la qual els punts homòlegs són dos punts inversos en l'esmentada inversió. Les rectes no euclidianes en H2 són els arcs de les circumferències ortogonals a SIGMA, exteriors a SIGMA i les rectes suports dels diàmetres de SIGMA exclosa la part interior a SIGMA (el diàmetre).

Hi ha triangles semblants als de les figures 1 i 2 com en PI; es diferencien en el fet que les circumferències en lloc de passar per P són ortogonals a una circumferència de centre P (la SIGMA d'aquesta figura). Tampoc no es compleix l'axioma de Pasch per a tots els triangles, hi ha triangles no paschians. En H2 , per anar d'alguns punts a uns altres s'ha de rodejar SIGMA, no es pot penetrar en SIGMA.

Una diferència topològica entre H1 i H2 és que en la primera les circumferències no euclidianes es representen per circumferències euclidianes interiors a H1 amb una definició distinta de centre, radi i diàmetre, mentre que en H2 les circumferències no euclidianes, la imatge de les quals no rodeja SIGMA, tenen el seu centre fora d'aquesta, el seu dibuix és semblant al de la figura 3, però els diàmetres en lloc de ser les circumferències que passen per D (el punt P del PI) són ortogonals a una circumferència de centre en D (la SIGMA d'aquesta figura). També són circumferències no euclidianes les parts de les rectes que no tallen SIGMA, exteriors a SIGMA. Això és per causa del fet que les circumferències de H2 són les inverses respecte a O (centre de SIGMA) de les circumferències de H1 , amb potència R2 (R radi de SIGMA) i per tant les circumferències que passen per O (interiors a SIGMA) es transformen en aquesta inversió en rectes no secants a SIGMA. En la figura 5 s'ha representat una d'aquestes, la circumferència que passa per O (interior a SIGMA) es transforma en aquesta inversió en la recta d, circumferència no euclidiana de H2 , el centre de la qual és el punt C (invers del centre de la circumferència de diàmetre OA), i els diàmetres són els arcs de les circumferències ortogonals a SIGMA que passen per C i es troben en el semiplà a la dreta de d.

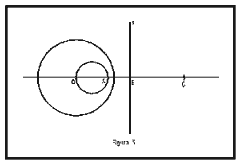
(fig. 5)

Si en els models anteriors se substitueix SIGMA per una circumferència (o una hiperesfera en el cas de n dimensions) imaginària, és a dir, R es canvia per iR (R2 per -R2 ) es tenen els models del pla (o de l'espai) el·líptic E1 i E2 , el segon no és simplement connex. En aquests models no hi ha paral·leles ni figures imaginàries, però sí que hi ha triangles conjugats reals, cosa aquesta última que no existeix en H1 i H2 ; PI, H2 i E2 estan en la mateixa relació amb E, H1 i E1 respectivament.

He fet el càlcul de la mètrica finita i diferencial angular que en el cas de tres dimensions estableix les relacions en un triedre entre els angles de les arestes i els angles diedres de les cares, que és summament curiosa.

En E1 , com en H1 , si R tendeix a zero, tendeixen a desaparéixer (a transformar-se en un punt) i si R tendeix a infinit, tendeixen a l'espai euclidià. En E2 com H2 , si R tendeix a infinit, tendeixen a desaparéixer, i si R tendeix a zero, tendeixen al pla o a l'espai inversiu incomplet. Per això podem anomenar aquests espais de curvatura infinita, perquè -1/R2 és la curvatura de l'espai.

En H1 els arcs interiors a SIGMA de les circumferències secants a SIGMA són les equidistants, mentre que els arcs exteriors són les equidistants de H2 . En l'espai euclidià les rectes paral·leles són equidistants i recíprocament si dues rectes són equidistants, són paral·leles. En el pla hiperbòlic les rectes paral·leles no són equidistants, la corba equidistant d'una recta no és una recta. Les equidistants d'una recta no euclidiana en H1 són les circumferències que tallen SIGMA en dos punts que pertanyen a la recta no euclidiana; entre les equidistants hi ha la corda de SIGMA determinada per la circumferència ortogonal a SIGMA imatge de la recta no euclidiana, com també per totes les seues equidistants.

Les circumferències tangents a SIGMA són les circumferències de radi infinit (horicicles). En el cas de tres dimensions són esferes tangents a la SIGMA i la geometria induïda en elles per la geometria de Lobatschewski és la geometria euclidiana. Si són interiors a SIGMA, pertanyen a H1 , i si són exteriors, a H2 .

Mitjançant una oportuna transformació geomètrica H1 i H2 es transformen conjuntament en un model H3 en el qual existeix una circumferència (o esfera fonamental) que és la mateixa SIGMA anterior i les rectes (o els plans) no euclidianes són les cordes de SIGMA (o els cercles de SIGMA) amb una mètrica distinta de H1 i H2 . En aquest model els punts imaginaris es troben sobre les rectes reals exteriors a SIGMA, interiors a les seues interseccions imaginàries amb SIGMA. Es dóna la circumstància que el suport dels punts imaginaris és una recta real, mentre que en H1 i H2 el suport dels punts imaginaris és una circumferència imaginària de centre real i radi imaginari. És un model que és simplement connex. El mateix passa amb E1 i E2 : que es transformen en un model E3 d'espai el·líptic (també simplement connex) en el qual les rectes (o els plans) no euclidianes són rectes o plans euclidians. En aquests espais H3 i E3 , les homologies tenen el paper que la inversió tenia en els anteriors.

Altres dos models H4 i H5 d'espais hiperbòlics i E4 i E5 d'espais el·líptics (figura 6), els he obtinguts sobre la superfície d'una esfera S. Si la tallem per un pla AB (que conté la recta AB i la perpendicular al pla del paper) S queda dividida en dos casquets, I (superior) i II (inferior), pel pla AB. Si tallem S per plans que passen per P (pol del pla AB) s'obté una circumferència amb un arc en I (model H4 ) i un altre en II (model H5 ) que són models del pla hiperbòlic amb una mètrica convenient sobre S; entre els punts dels quals existeix una bijecció, la dels punts alineats amb P. Aquests arcs de circumferències són les rectes no euclidianes.

(fig. 6)

Si projectem des de D (en el diàmetre PQOD, O és el centre de S) el casquet I superior sobre el pla tangent en C (projecció estereogràfica), obtenim el model H2 , i si projectem el casquet II inferior, obtenim el model H1 ; passa el contrari si efectuem la projecció des de C sobre el pla tangent a S en D. Les seccions pel pla AB dels plans que passen per P donen el model H3 . Les transformacions geomètriques anteriors donen les relacions entre punts homòlegs dels models H1 a H5 . En H4 i H5 les rectes imaginàries són les circumferències imaginàries interseccions de S amb els plans que passen per P exteriors a S i per tant al con circumscrit a S des de P.

Si en les operacions anteriors se substitueix el punt P pel punt Q, s'obtenen sobre els casquets I i II els models E4 i E5 del pla el·líptic sobre S. Les projeccions estereogràfiques des de D i C donen els models E2 i E1 , i les interseccions dels plans tangents en D o C a S amb els plans que passen per Q donen el model E3 .

He denominat aquesta teoria de les n-esferes incompletes. Hi ha dos casos particulars que ja eren coneguts: un model de Poincaré quan P es troba a l'infinit, i el clàssic del pla de Riemann quan Q coincideix amb el centre O de S.

Els angles en els models H4 , H5 , E4 , E5 són els euclidians.

Quan P es troba sobre S les interseccions de S amb els plans que passen per P, amb una mètrica convenient, donen un model del pla euclidià i la projecció estereogràfica des del punt de S diametralment oposat a P dóna un model del pla inversiu.

Les mètriques en H4 , H5 , E4 i E5 , i en el cas del paràgraf anterior, les he calculades.

En tots els casos no es compleix l'axioma de Pasch en les geometries euclidiana i no euclidiana (el·líptica o hiperbòlica) sobre espais que no siguen simplement connexos ja siga la connexió lineal o superficial, perquè existeixen triangles no paschians.

Com hem dit abans, Hilbert en Els fonaments de la geometria dóna l'axiomàtica de la geometria euclidiana i del pla hiperbòlic, però no la de l'el·líptic. Al meu parer només és vàlida per a espais simplement connexos.

Com que en el pla el·líptic no es compleix l'axioma d'Arquimedes i no existeixen rectes paral·leles, al meu parer es pot establir l'axiomàtica del pla el·líptic de la manera següent:

són vàlids:
A) Els axiomes d'enllaç, d'ordenació i de congruència de Hilbert per al pla hiperbòlic.
B) No són vàlids ni el V postulat d'Euclides ni l'axioma de les rectes secants i no secants de Hilbert. S'han de substituir per l'axioma següent: "dues rectes qualssevol es tallen en un punt".
C) No és vàlid l'axioma d'Arquimedes. S'ha de substituir per l'axioma de la divisibilitat indefinida. És vàlid l'axioma de continuïtat de la plenitud.

Altres vegades, en tractar del que he anomenat funció s(x) i j(x), he parlat de la crisi del principi d'identitat. Però també el principi d'identitat, a més del principi d'igualtat per superposició o encaix, entren en crisi en la geometria hiperbòlica. Davant els processos de límit que tenen lloc sense memòria, en els quals una vegada assolit el límit s'esborra el procés pel qual va ser assolit, hi ha altres processos de límit en els quals el comportament del límit depén de la història del seu procés.

Aclarim el paràgraf anterior amb un exemple. En el model H1 un punt en el cercle SIGMA és de tal manera que si dos punts estan superposats, són idèntics i la distància entre ells és zero; però si un punt es troba en la circumferència frontera de SIGMA, es troba a distància infinita de qualsevol punt del cercle SIGMA, per petita que siga la distància euclidiana que els separa. Si dos punts estan superposats en la circumferència frontera de SIGMA, encara que l'un estiga encaixat en l'altre, no són totalment idèntics, i es troben a una distància finita, que és una indeterminació del tipus infinit-infinit, que s'ha de calcular igual, encara que de manera distinta, com en anàlisi matemàtica s'estén una indeterminació de infinit-infinit per la regla de L'Hôpital.

Per exemple, una recta no euclidiana D i una de les seues equidistants G són en els models H1 i H2 dues circumferències (la D ortogonal a SIGMA) que es tallen en dos punts de SIGMA; si A és un d'aquests punts considerat de D, és distint de considerat de G, encara que estiguen superposats, la seua distància és igual a la distància constant que separa D de G al llarg de tot el seu recorregut. El punt A es pot assolir com a punt límit en dos moviments en els quals un mòbil recorre D i un altre recorre G sent equidistants en tot el moviment, i així queden en assolir la seua mateixa posició límit A sobre SIGMA; es conserva la memòria de com s'ha assolit aquesta posició límit, es recorda la seua història. El concepte del punt límit A és dinàmic i no estàtic i aleshores la superposició no significa igualtat. El que s'ha dit va en contra de l'axioma IV d'Euclides que afirma "coses que encaixen cadascuna en l'altra són iguals", axioma admés en l'actualitat.

Les equidistants es manegen bé en H1 i H2 perquè són circumferències que poden degenerar en cordes, mentre que en H3 són el·lipses bitangents a SIGMA, equidisten de la corda de SIGMA (recta no euclidiana) que uneix els dos punts de contacte de cada el·lipse amb SIGMA.

H3 té moltes aplicacions a la Teoria de la Relativitat. A la magnitud de la velocitat que resulta de compondre dues velocitats coplanàries segons la fórmula d'Einstein, li he donat una forma intrínseca que és vàlida en qualsevol nombre de dimensions. Aplicada a dues velocitats infinitament pròximes, m'ha permés calcular l'element lineal (el dr) de l'espai de les velocitats relativistes, que és un espai hiperbòlic H3 , i com que les velocitats han de ser inferiors a un límit (la velocitat de la llum en el buit) em permet construir una mecànica estadística relativista, que es desvia significativament de l'estadística clàssica, per a temperatures molt altes, com per exemple les que hi ha a l'interior d'alguns astres o de les seues explosions.

He donat una forma intrínseca a la composició vectorial de velocitats relativistes en dues dimensions, que es pot generalitzar a n dimensions, i aplicada a dues velocitats infinitament pròximes, he definit allò que he anomenat diferencial d'Einstein-Lobatschewski, denotat per Dv, que té la propietat que el producte escalar Dv·Dv és igual al dr2 de l'espai hiperbòlic, així com el producte escalar dv·dv és igual al dr2 de l'espai euclidià, quan dv és el diferencial ordinari d'un vector.

Les fórmules anteriors són vàlides en un espai de Hilbert, de manera que es pot investigar un espai de Hilbert-Lobatschewski, i juntament amb aquest espai de Hilbert hiperbòlic existeix també un espai el·líptic.

Moltes gràcies a la Universitat Politècnica de València per haver-me nomenat doctor honoris causa i a tots vostés per haver-me acompanyat en aquest acte.